Volltreffer - Details: Mathematische Hintergründe
Bevor du diesen Artikel liest, solltest du den Volltreffer-Artikel sorgfältig durchgelesen haben. Dieser ist zum Verständnis notwendig.
Am Ende unseres Volltreffer-Artikels haben wir die Behauptung aufgestellt, dass Volltreffer als gezieltes taktisches Mittel unterschätzt werden. Diese Behauptung soll hier mit mathematischen Belegen untermauert werden.
Um die Chance zu berechnen, nach einer Anzahl von n Angriffen mit einer bestimmten Attacke mindestens einen Volltreffer zu landen, wird folgende Formel verwendet:
![]()
Dabei gilt:
P... Chance auf zumindest einen Volltreffer in Prozent
n... Anzahl Angriffe mit der Attacke (Runden)
q... Chance auf einen Volltreffer in einer Runde in Prozent (mehr dazu im Volltreffer-Artikel)
Damit du nicht alle möglichen Werte durchrechnen muss, sind in der folgenden Tabelle alle Werte für 25 Runden berechnet (länger wird ein Pokémon nicht im Kampf bleiben).
| n/p | 6,5 | 12,5 | 25 | 33,2 | 50 |
|---|---|---|---|---|---|
| 1 | 6,5 | 12,5 | 25 | 33,2 | 50 |
| 2 | 12,6 | 23,4 | 43,8 | 55,4 | 75 |
| 3 | 18,3 | 33 | 57,8 | 70,2 | 87,5 |
| 4 | 23,6 | 41,4 | 68,4 | 80,1 | 93,8 |
| 5 | 28,5 | 48,7 | 76,3 | 86,7 | 96,9 |
| 6 | 33,2 | 55,1 | 82,2 | 91,1 | 98,4 |
| 7 | 37,5 | 60,7 | 86,7 | 94,1 | 99,2 |
| 8 | 41,6 | 65,6 | 90 | 96 | 99,6 |
| 9 | 45,4 | 69,9 | 92,5 | 97,4 | 99,8 |
| 10 | 48,9 | 73,7 | 94,4 | 98,2 | 99,9 |
| 11 | 52,3 | 77 | 95,8 | 98,8 | 100 |
| 12 | 55,4 | 79,9 | 96,8 | 99,2 | 100 |
| 13 | 58,3 | 82,4 | 97,6 | 99,5 | 100 |
| 14 | 61 | 84,6 | 98,2 | 99,6 | 100 |
| 15 | 63,5 | 86,5 | 98,7 | 99,8 | 100 |
| 16 | 65,9 | 88,2 | 99 | 99,8 | 100 |
| 17 | 68,1 | 89,7 | 99,2 | 99,9 | 100 |
| 18 | 70,2 | 91 | 99,4 | 99,9 | 100 |
| 19 | 72,1 | 92,1 | 99,6 | 100 | 100 |
| 20 | 73,9 | 93,1 | 99,7 | 100 | 100 |
| 21 | 75,6 | 93,9 | 99,8 | 100 | 100 |
| 22 | 77,2 | 94,7 | 99,8 | 100 | 100 |
| 23 | 78,7 | 95,4 | 99,9 | 100 | 100 |
| 24 | 80,1 | 95,9 | 99,9 | 100 | 100 |
| 25 | 81,4 | 96,5 | 99,9 | 100 | 100 |
| 50 | 96,5 | 99,9 | 100 | 100 | 100 |
| 100 | 99,9 | 100 | 100 | 100 | 100 |
Was sind die wichtigsten Erkenntnisse daraus?
- Volltreffer kommen selbst dann relativ häufig vor, wenn man ausschließlich normale Attacken (6,5% Volltreffer-Chance pro Runde) verwendet. Bereits nach 10 Angriffen (und die meisten Kämpfe dauern wesentlich länger), gab es zu 49% mindestens einen Volltreffer.
- In drei Runden beträgt die Volltreffer Chance für normale Attacken 18,3%. Volltreffer-Attacken (Chancen mit erhöhter Volltrefferwahrscheinlichkeit, d.h. 25%) haben zu diesem Zeitpunkt bereits zu 57,8% einen Volltreffer erzielt. Mit der Score-Linse zusätzlich wären es gar 70,2%.
Die Tabelle wird noch in der nachfolgenden Graphik veranschaulicht:
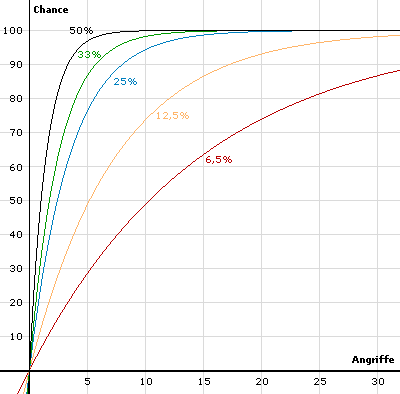
Man sieht also auch, dass sich bereits der Einsatz einer Scope-Linse, welcher die Volltrefferchance um einen Level steigen lässt, auszahlt. Volltreffer können stets eine Wende im Spiel darstellen. Du verzichtest dafür auf die Verwendung von Überresten. Dein Pokémon besitzt dadurch etwas weniger Staying Power, kann dafür den Gegner schneller besiegen. Eine konkrete Formel, wann sich der Einsatz auszahlt gibt es jedoch nicht. Als Richtlinie kannst du verwenden: Pokémon, die von Haus aus eine geringe Staying-Power aufweisen, sollten stärker auf Volltreffer setzen. Bei Pokémon mit niedriger Staying-Power haben Überreste ohnehin weniger positive Auswirkungen als bei echten Tanks und Stallern.
Anzahl Volltreffer in n Runden
Bisher haben wir uns nur mit der Wahrscheinlichkeit beschäftigt, mindestens einen Volltreffer zu erzielen. Natürlich kann es auch mehr als einen Volltreffer geben. Die Wahrscheinlichkeit, a Volltreffer in n Runden bei einer Volltrefferwahrscheinlichkeit von p pro Runde zu erzielen, beträgt:
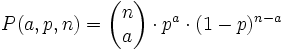
Für diese Berechnung braucht man den Binomialkoeffizienten. Wer nicht weiß, wie man diesen berechnet, kann unsere Tabellen verwenden. Diese kannst du als im Download im Excel-Format bekommen. Wenn du kein Excel hast, kannst du auch OpenOffice, welches hier gratis zum Download steht, verwenden.
In den folgenden beiden Tabellenausschnitten kannst du nachsehen, wie hoch die Wahrscheinlichkeit auf eine bestimmte Trefferanzahl nach 10 bzw. 20 Runden ist.
Nach 10 Runden:
| p/n | 0 | 1 | 2 | 3 | 4 | 5 | mehr |
|---|---|---|---|---|---|---|---|
| 6,5% | 51,1 | 35,5 | 11,1 | 2,1 | 0,3 | 0 | 0 |
| 12,5% | 26,3 | 37,6 | 24,2 | 9,2 | 2,3 | 0,4 | 0 |
| 25% | 5,6 | 18,8 | 28,2 | 25 | 14,6 | 5,8 | 2 |
| 33,2% | 1,8 | 8,8 | 19,7 | 26,1 | 22,7 | 13,5 | 7,4 |
| 50% | 0,1 | 1 | 4,4 | 11,7 | 20,5 | 24,6 | 37,7 |
Nach 20 Runden:
| p/n | 0 | 1 | 2 | 3 | 4 | 5 | mehr |
|---|---|---|---|---|---|---|---|
| 6,5% | 26,1 | 36,3 | 23,9 | 10 | 3 | 0,7 | 0,1 |
| 12,5% | 6,9 | 19,8 | 26,8 | 23 | 14 | 6,4 | 3,1 |
| 25% | 0,3 | 2,1 | 6,7 | 13,4 | 19 | 20,2 | 38,3 |
| 33,2% | 0 | 0,3 | 1,5 | 4,4 | 9,3 | 14,7 | 69,8 |
| 50% | 0 | 0 | 0 | 0,1 | 0,5 | 1,5 | 97,9 |
Wenn du wissen willst, wie viele Volltreffer du dir bei einer Volltrefferchance p bei n Angriffen erwarten darfst, kannst du die folgende Formel verwenden.
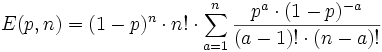
Durch Umformungen oder experimentelles Einsetzen findet man heraus, dass man den Erwartungswert (durchschnittliche Anzahl der Volltreffer) in diesem Fall durch den einfachen, linearen Zusammenhang ![]() ausdrücken kann. Die wichtigsten Werte sind außerdem in folgender Tabelle eingetragen:
ausdrücken kann. Die wichtigsten Werte sind außerdem in folgender Tabelle eingetragen:
| 6,50% | 12,50% | 25% | 33,20% | 50% | |
|---|---|---|---|---|---|
| 1 | 0,07 | 0,13 | 0,25 | 0,33 | 0,5 |
| 2 | 0,13 | 0,25 | 0,5 | 0,66 | 1 |
| 3 | 0,2 | 0,38 | 0,75 | 1 | 1,5 |
| 4 | 0,26 | 0,5 | 1 | 1,33 | 2 |
| 5 | 0,33 | 0,63 | 1,25 | 1,66 | 2,5 |
| 6 | 0,39 | 0,75 | 1,5 | 1,99 | 3 |
| 7 | 0,46 | 0,88 | 1,75 | 2,32 | 3,5 |
| 8 | 0,52 | 1 | 2 | 2,66 | 4 |
| 9 | 0,59 | 1,13 | 2,25 | 2,99 | 4,5 |
| 10 | 0,65 | 1,25 | 2,5 | 3,32 | 5 |
| 15 | 0,98 | 1,88 | 3,75 | 4,98 | 7,5 |
| 20 | 1,3 | 2,5 | 5 | 6,64 | 10 |
| 25 | 1,63 | 3,13 | 6,25 | 8,3 | 12,5 |
| 30 | 1,95 | 3,75 | 7,5 | 9,96 | 15 |
| 35 | 2,28 | 4,38 | 8,75 | 11,62 | 17,5 |
| 40 | 2,6 | 5 | 10 | 13,28 | 20 |
| 45 | 2,93 | 5,63 | 11,25 | 14,94 | 22,5 |
| 50 | 3,25 | 6,25 | 12,5 | 16,6 | 25 |
| 55 | 3,58 | 6,88 | 13,75 | 18,26 | 27,5 |
| 60 | 3,9 | 7,5 | 15 | 19,92 | 30 |
| 65 | 4,23 | 8,13 | 16,25 | 21,58 | 32,5 |
| 70 | 4,55 | 8,75 | 17,5 | 23,24 | 35 |
| 75 | 4,88 | 9,38 | 18,75 | 24,9 | 37,5 |
| 80 | 5,2 | 10 | 20 | 26,56 | 40 |
| 85 | 5,53 | 10,63 | 21,25 | 28,22 | 42,5 |
| 90 | 5,85 | 11,25 | 22,5 | 29,88 | 45 |
| 95 | 6,18 | 11,88 | 23,75 | 31,54 | 47,5 |
| 100 | 6,5 | 12,5 | 25 | 33,2 | 50 |
Wie man daraus erkennt, kann man durch Erhöhen der Volltrefferquote mittels Scope-Linse oder den Einsatz von Volltreffer Attacken (oder beides kombiniert) ziemlich sicher Volltreffer herbeiführen. Das hat nichts mehr mit reinem Glück zu tun, sondern kann gezielt eingesetzt werden.
Überreste oder Scope-Linse
Bei Sweepern stellt sich nun die Frage, ob man als Item besser Überreste oder die Scope-Linse verwenden sollte. Allgemein sagt man, Überreste wären wesentlich besser – das stimmt so jedoch nicht. Die beiden Items sind in etwa gleichwertig und man muss die Sache schon ein wenig differenzierter Ansehen.
Verwende Überreste für...
- Langlebige Sweeper
- Sweeper, die Wertsteigerungen (Boost Ups) verwenden
- Sweeper in Sandsturm-Teams
Verwende Scope-Linse für...
- Sweeper mit niedriger Staying Power
- Sweeper, mit denen man auf Risiko gehen will
Vergiss jedoch nicht, dass es noch andere Items wie zum Beispiel Wahlband, Flinkklaue und Kingstein gibt, deren Einsatz auch oft Vorteile mit sich bringt.